前言
随着数字科技的发展,FIR处理器在音频系统优化中使用越来越普遍。
FIR(有限脉冲响应)滤波器是一种数字滤波器,其工作基础是将输入信号与一组固定的系数(通常称为滤波器系数或冲激响应)进行卷积运算,从而得到输出信号。与 IIR 滤波器(无限冲激响应滤波器)不同,FIR 滤波器的冲激响应是有限的,因此其系统是稳定的,并且具有线性相位,这使得 FIR 滤波器在音频处理等领域具有特别重要的应用。
在实际应用中,很多工程师会借助工具来设计 FIR 滤波器。以谛听声学仿真测量软件为例,它具有自动FIR功能,能根据设定的目标曲线自动生成FIR滤波器参数,我们在使用过程中,会发现当选择好滤波器的抽头数后,软件会自动显示对应的FIR最低有效处理频率(频率分辨率的3倍),为什么FIR真正能起作用的下限,不是我们通常所说的“频率分辨率”,而是它的 3 倍呢?今天我们来谈谈这个话题。
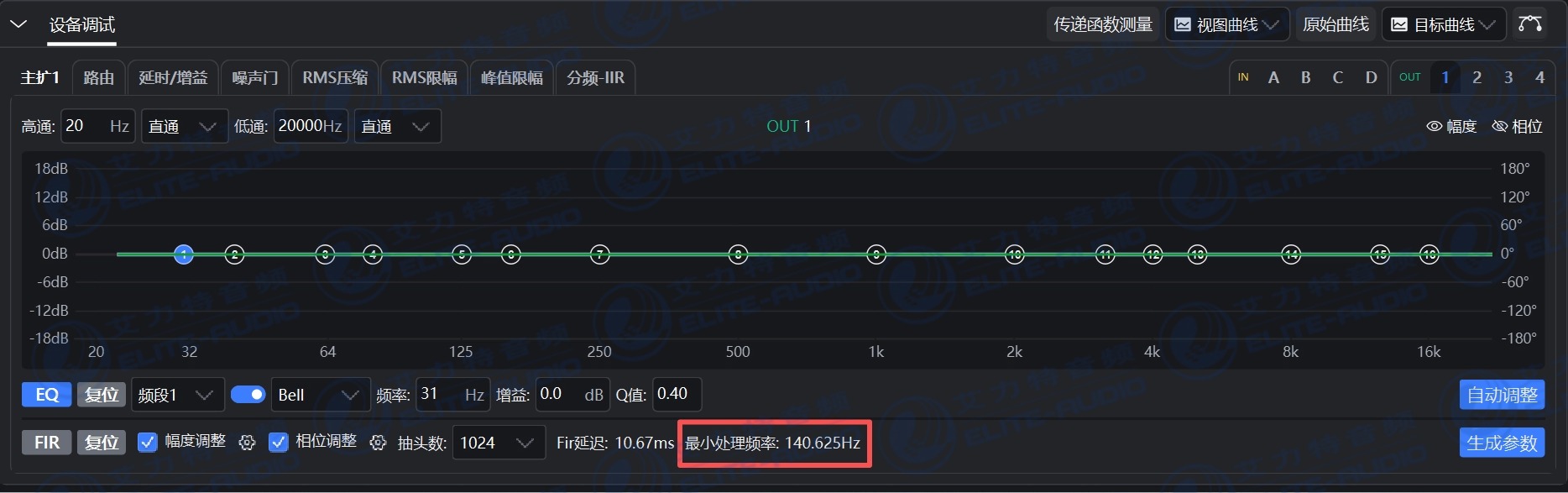
一、频率分辨率的计算
我们先来看FIR“频率分辨率”(即最小可区分的频率间隔)的计算,FIR 滤波器的频率分辨率Δf与阶数 N和采样率 fs 有关:
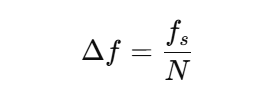
这个公式看起来很直接。例如,采样率 48 kHz,滤波器阶数 1024,那么:
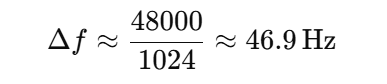
这意味着滤波器在频域上好像能“精确”到 47 Hz 的分辨率。很多初学者会据此认为滤波器可以从 47 Hz 开始有效工作。但现实并非如此。
二、过渡带与窗函数
在 FIR 滤波器的频率响应中,过渡带是非常重要的一个概念。过渡带指的是通带到阻带之间的区域,即从信号完全通过的频率区间到信号完全被抑制的频率区间之间的过渡区。FIR 滤波器的实际频率响应并非简单的在每个分辨点上产生陡峭的变化。相反,滤波器的频率响应通常会在过渡带内逐渐过渡,尤其是在通带和阻带之间的过渡区。
由于 FIR 滤波器并不能像理想滤波器那样突然切换(即从 0 到 -∞),因此在过渡带中,滤波器的增益会逐渐下降。这种过渡区的宽度与窗函数的选择密切相关。窗函数的主瓣宽度决定了过渡带的宽度。窗函数的主瓣越宽,过渡带就越宽,如果过渡带过于窄,滤波器将无法实现理想的通带和阻带响应,导致性能下降。
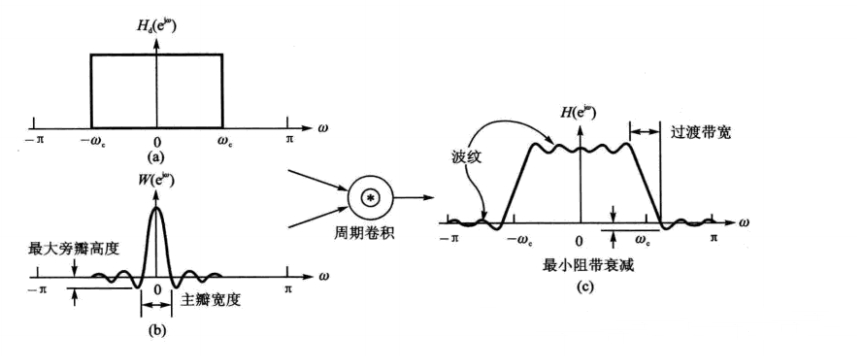
三、为什么频率分辨率乘以3?
这里就是我们讨论的关键:FIR 滤波器的频率响应受到窗函数的影响,而窗函数的 主瓣宽度直接决定了滤波器的过渡带宽度。不同窗函数的主瓣宽度通常是频率分辨率的倍数,这段宽度决定了滤波器无法“比它更窄”地分辨频率,换句话说,它就是滤波器过渡带的下限。
例如,使用矩形窗时,主瓣宽度大约是 2倍的Δf(频率分辨率),而汉宁窗和汉明窗的主瓣宽度约为4倍的Δf(频率分辨率),这就决定了过渡带的宽度,影响滤波器的有效频率范围。目前大部分常见窗函数的主瓣宽度大约是频率分辨率的 2 到 4 倍。这个乘数可以确保滤波器的实际性能更接近需求,而不会过度乐观地设计过于窄的过渡带。
基于这些情况,项目实践中,工程师通常会发现 3倍的频率分辨率是一个较为保守且实际可行的估算值。这意味着,尽管理论上频率分辨率为 Δf,但实际的有效控制范围往往需要 乘以 3 才能确保滤波器能够有效工作,特别是低频部分,在对数坐标体系下由于频率较疏,低频的过渡带宽度通常较大,因此它们的处理能力较差,当滤波器阶数不够高时,低频信号的响应可能会出现明显的波动和失真。
还是上面那个例子:48 kHz 采样率,1024 阶 FIR。
▪️理论分辨率:Δf=46.9 Hz
▪️乘以 3 后:FIR作用下限频率约 140 Hz
四、总结
对工程师而言,FIR 滤波器作用下限 ≈ 频率分辨率 × 3,是一个非常实用的经验法则。它基于窗函数主瓣宽度与过渡带的特性,帮助我们更真实地估计滤波器的低频控制能力。谛听声学仿真测量软件正是基于这一规律,在自动 FIR 功能中根据抽头数给出合理的最低下限频率,帮助工程师们快速判断滤波器最低有效可控频率,减少不必要的复杂计算,让滤波器在实际应用中达到最佳效果。
